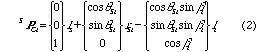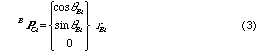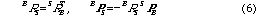パラレルメカニズムを用いた
高速・高精度三次元座標計測システム
静岡大学 ○大岩 孝彰 静岡大学(院) 久利 直道
要 旨
従来の直交座標型とは異なるパラレルメカニズムを用いた三次元空間座標測定機を提案する.このメカニズムでは従来の直交座標型すなわちシリアルメカニズムの持っていた欠点を改善できるため,高剛性・高速・高精度を実現できると考えられる. 本報ではまず提案するシステムの原理を示し,機構の総合を行う.さらにリンクの長さから測定点の座標値を求めるための順運動学解析を行い,それを用いて測定領域を計算した.
はじめに
近年,複雑な形状を持つ機械部品等の高精密加工および精密測定の要求が著しく高まっている.現在,このような部品は直交座標型の三次元測定機(図1 )で測定されることが多いが,精度的および能率的に限界に達している.それはこの測定機の基本構造が
1.精密測定の基本であるアッベの原理に反する.
2.剛性の低い(片持ち)梁構造を採っている.
3.各移動軸の位置決めおよび測定誤差が累積される.
4.質量増により移動速度が低い.
などに起因している.
従来とは異なる原理の三次元座標計測システムとして,レーザスキャナまたはレーザ干渉計を用いた光学的方法1)〜4),超音波を用いる方法5), 6)などが研究されている.これらの方法では機械的な可動部の負担が少ないため,高速度な計測が可能である.反面,空気のゆらぎ・温度変化などの影響を受けやすく,より精度を向上させることは困難である.
本研究では,従来の直交座標型とは異なるパラレルリンクメカニズムを用いた三次元座標測定システムを提案する.このメカニズムでは上述の四つの問題を回避できるため,剛性,精度,速度などの面で有利であり,形状測定の高精度化・高速化が可能であると考えられる.本報では本システムの特長および運動学解析結果について報告する.
原 理
提案する三次元座標測定機の概略を図2 に示す. 三本の脚の中には脚を伸縮させるアクチュエータと測長器を内蔵する.この3本の脚の長さをそれぞれ変化させると上部のステージは3自由度の運動をし,ステージに取り付けられたタッチプローブの位置と姿勢は一意に決定される.したがって,プローブが測定対象に触れた瞬間の三本の脚の長さよりプローブの三次元座標位置を計算することが可能となる.
提案する本方式では,従来の直交型と比較して,
1.三辺測量方式はアッベの原理に反していない.
2.トラス構造のため剛性が高い.
3.各軸の誤差が累積しない(誤差平均化).
4.慣性質量を小さくでき,移動速度が高い.
などの特長がある.
空間閉ループ機構の数の総合
一般に空間閉ループ機構の自由度は,Grulerの公式7)を用いて求められる.

ここでFは機構の自由度の総数,lはステージとベースを含めたリンクの数,nは関節の総数, fiはi番目の関節の自由度の数である.本報では閉ループの数(=脚の数)を3,それぞれのループの関節の配置は同じとして,F=3すなわち自由度が3となるためのすべての関節の自由度と配置を図3 に示す.関節の数に関わらず,関節の自由度の総数Σfiが15となるように設計すればよいことがわかった.採用した図2の機構は1-1-3であり,l=8,n=9,fi=5(i=1〜3)であるからF=3となる.
順運動学解析
一般にパラレルメカニズムの順運動学はシリアルメカニズムのそれとは逆に非常に複雑となり,解析的に求められない場合が多い(本機構では逆運動学も困難である).まず,座標系を図4 のようにとると,プローブに固定された座標系ΣSでは関節Ci点の位置ベクトルSPCi は,
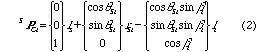
一方,ベース座標系ΣBでは
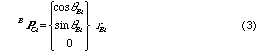
である. ΣSから見たΣBの位置ベクトルをSPB ,回転変換行列をSRBとして,これをΣS系で表すと,

となる.ここで式(2)と(4)は等しいから結局,

となり,i=1〜3であるから計9式が得られる.この連立方程式の未知数は SPB , SRBおよびβiの9個となるが,非線形となるため,解析的に根を求めることは困難である.このため,まず式(2)と(3)から数値解法によりβiを求め, SRB の成分を方向余弦で表すと式(5)は9変数の線形連立方程式となり,容易に解くことが可能となる.以上より求められたSPB , SRBよりプローブの位置と姿勢BPS ,BRS は次の式より求められる.
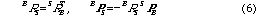
測定領域
以上の順運動学を用いて測定作業領域を計算した.図4におけるrS=50mm,rB=500mm,lS=100mmとし,脚の長さliを800〜1250mm(ストローク450mm)としたときの座標をプロットした.球面軸受けの揺動角度の制限は考慮していない.図5(a) はZ方向から見た様子を示している.また図(b) はX-Z平面でプロットした結果である.このようにパラレルメカニズムでは作業領域は直方体形状ではなく評価が困難であるが,およそX500×Y500×Z200mm程度の測定領域であることが推察される.
おわりに
従来の直交座標型とは異なる三次元座標測定機を提案し,原理について述べた.またリンクの長さから測定点の座標値を求めるための順運動学解析を行い,測定作業領域を計算した.本研究は高度自動化技術振興財団の平成7年度研究助成金で行われた.記して謝意を表する.
参考文献
1) 大岩他2名:精密工学会誌,59巻2号(1993)305-310.
2) K. Lau et al. : Precision Engineering, Vol.8, No.1(1986)3-8.
3) 中村他4名:精密工学会誌,57巻5号(1991)831-836.
4) J.H.Gilby et al. : Sensor Review, October (1982) 180-184.
5) H. Peremans :IEEE Trans. Robotics Automat., vol. 9, No.1, (1988)36-48.
6) 青柳他:精密工学会誌,58巻5号(1992)859-864.
7) K. Hunt :Kinematic Geometry of Mechanisms, Oxford Press(1978).